This webpage contains information about my doctoral thesis entitled “Spreading phenomena on complex networks and social systems”. The full text is available here.
Divulgado no site oficial da Sociedade Brasileira de Física neste link.
A tese recebeu o Prêmio Professor José Leite Lopes de Melhor Tese de Doutoramento de 2021 da seleção de teses defendidas em 2020. A Comissão Avaliadora foi composta por Prof. Eduardo Miranda (Coordenador) – Unicamp, Profa. Miriam Mendes Gandelman (UFRJ), Prof. Olival Freire Jr. (UFBA), Prof. Francisco Aparecido Rodrigues (ICMC-USP) e Prof. Luis Guilherme de Carvalho Rego (UFSC), além de ter sido premiada na Comissão de Física Estatística e Computacional.
Slides in English, audio in Portuguese. Click here.
Resumo estendido da tese
A disseminação de epidemias tem sido um problema constante em toda a história da humanidade, e é um dos mais proeminentes e amplamente investigados na literatura recente de sistemas complexos. Uma epidemia pode ser entendida como um fenômeno emergente a partir de interações locais de indivíduos, levando a um estado com um grande número de indivíduos ou elementos afetados por uma doença, informação ou outro ente que possa se espalhar. Usualmente esses processos são investigados por meio de equações diferenciais que assumem hipóteses simples como uma mistura homogênea, na qual todos os indivíduos de um sistema interagem com todos os demais, ou outros padrões de contato mais simples.
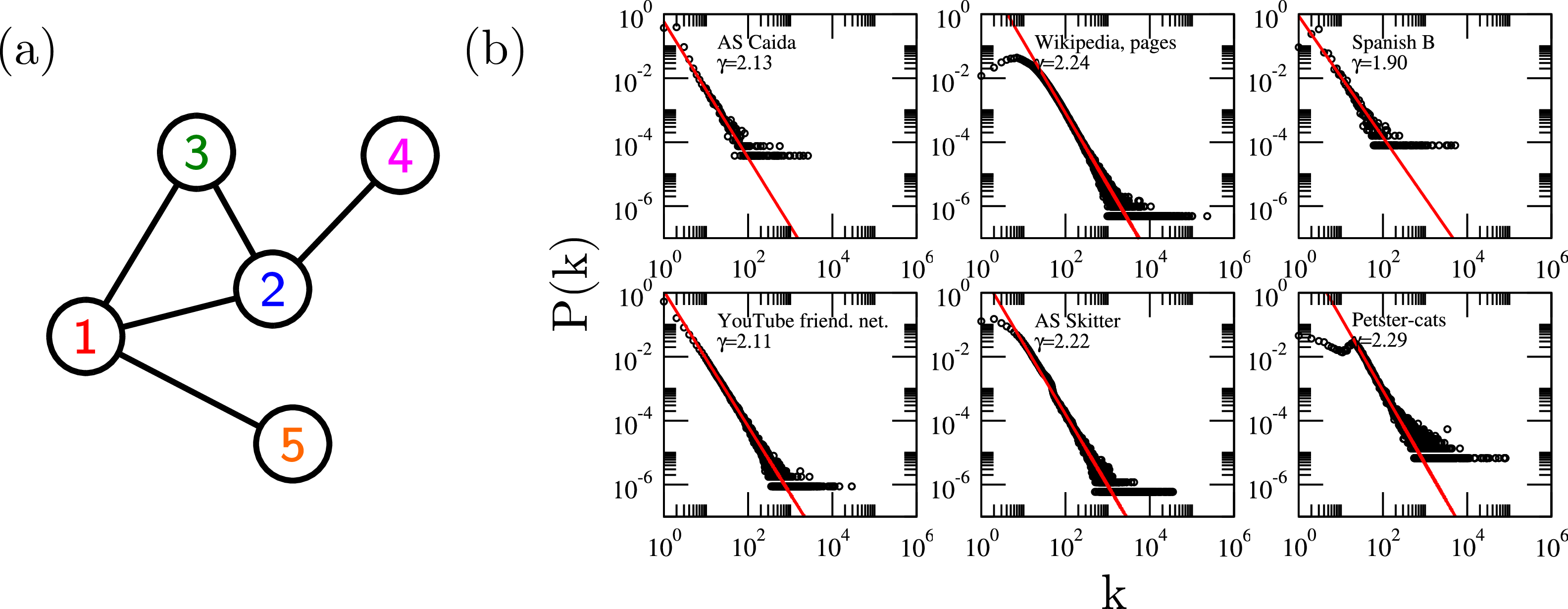
Figura 1: Exemplo de uma rede e distribuições de grau . (a) Rede com 5 vértices e 5 arestas, na qual o vértice 1 tem um grau . (b) Distribuição de grau para algumas redes reais, ajustes em lei de potência e seus expoentes . Mais detalhes nas Figuras 2.2 e 2.7 da Tese.
Entretanto, nossa vida é permeada por sistemas altamente conectados, como nas interações que regulam processos celulares nos seres vivos, as conexões entre neurônios no cérebro, diferentes infraestruturas de transporte nas quais nos movemos, e redes sociais online pelas quais nos comunicamos e recebemos informações. Cada um desses sistemas pode ser descrito por meio de uma rede complexa, que utiliza conceitos da teoria de grafos para representar matematicamente os elementos como vértices que interagem por meio de arestas, como na Figura 1(a). Muitas propriedades de conectividade desses sistemas são universais, compartilhadas entre os mais diferentes tipos de redes reais como as citadas anteriormente. Uma delas é a propriedade de mundo pequeno, que indica que é possível encontrar um caminho curto entre quaisquer dois elementos de um sistema facilmente. Isso ocorre, por exemplo, ao encontrar rotas de voos entre as principais cidades no mundo inteiro, permitindo cruzar todo o planeta em apenas algumas horas. Outra propriedade importante é que essas redes são livres de escala, relacionada ao fato de que a distribuição do grau ou número de conexões que cada elemento possui segue uma lei de potência , na qual é um expoente que afeta fortemente seus -ésimos momentos . Em particular, são encontrados hubs, vértices com grau muito maior que a média, e variância grande ou infinita, já que .
Após introduzir conceitos de redes complexas no Capítulo 2, nesta Tese são abordadas questões relacionadas aos aspectos fundamentais de processos dinâmicos nessas estruturas. Assumindo que cada vértice da rede possa assumir um estado, como suscetível ou infectado em uma dinâmica epidêmica, equações mestras podem ser construídas para obter as transições entre diferentes estados ao longo do tempo. Em processos de propagação de epidemias, somente infectados podem transmitir um ente para os demais por meio de interações como as representadas por arestas nas redes. Uma vez que não existam mais infectados, é possível chegar a um estado absorvente, do qual não há como sair sem um estímulo externo. Assim, todos os processos descritos nesta tese são de não equilíbrio, necessitando tratamentos analíticos e computacionais da Física Estatística de sistemas fora do equilíbrio. Sobretudo, ao utilizar estruturas de redes complexas para representar as interações nesses tipos de processos é muito difícil escrever equações diferenciais que os descrevam corretamente, necessitando recorrer a teorias de campo médio para tal. Como alternativa, são utilizadas simulações estocásticas por meio de algoritmos de Gillespie, que levam a resultados estatisticamente equivalentes aos que seriam obtidos por meio das equações mestras verdadeiras, e são comparadas com teorias de campo médio com análises de decaimento, espalhamento e quase-estacionárias. Como produto desta Tese, um artigo [1] propõe uma otimização desses algoritmos ao introduzir "processos fantasmas", que permitem simular processos dinâmicos em redes complexas muito grandes e com alto nível de heterogeneidade. Esses e outros detalhes a respeito de processos dinâmicos são encontrados no Capítulo 3 da Tese, juntamente com discussões sobre expoentes críticos.
Os principais resultados da Tese são apresentados em duas partes nos Capítulos 4 até o 7. A primeira é dedicada ao estudo da criticalidade no espalhamento de epidemias em redes complexas, começando com uma investigação sobre propriedades fundamentais de modelos suscetível-infectado-suscetível (SIS) [2], e depois na identificação de Fases de Griffiths em redes complexas modulares [3,4]. Já a segunda parte é voltada a aplicações da modelagem de epidemias em sistemas reais, iniciando com a criação de um método para quantificar câmaras de eco em redes sociais [5] e depois com modelagem dirigida por dados para estudar epidemias utilizando dados de mobilidade humana, demografia e padrões de contato na determinação das condições necessárias para o surgimento de um estado endêmico em função da mobilidade [6].
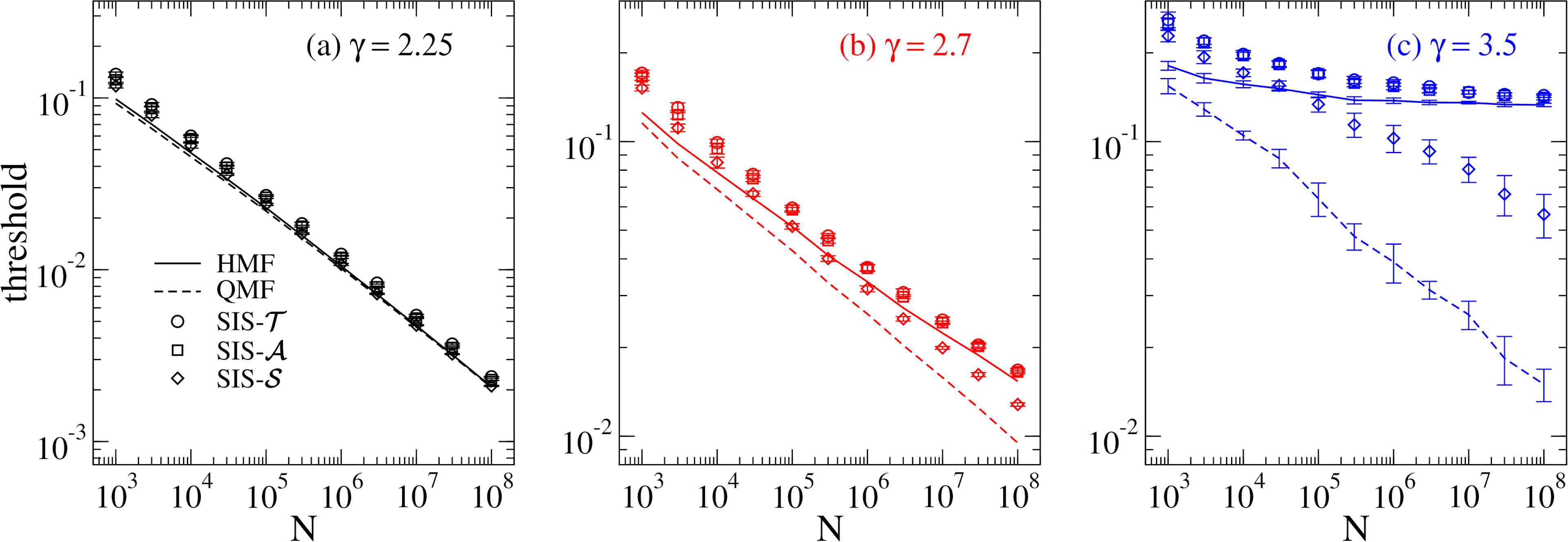
Figura 2: Limiares epidêmicos para os três modelos suscetível-infectado-suscetível (SIS) e teorias de campo médio para (a) , (b) e (c) . Note que todas concordam entre si para , levam a limiar nulo no limite termodinâmico em (a) e (b), mas com comportamentos diferentes para . Já para em (c), o modelo SIS- resulta em um limiar tendendo a zero de acordo com a teoria QMF, enquanto os modelos modificados tendem a um limiar finito predito pela teoria HMF.
O modelo SIS assume que cada elemento pode estar em dois estados: suscetível ou infectado. Nesse modelo, agentes infectados transmitem o ente com taxa para cada uma de suas conexões, e tornam-se suscetíveis espontaneamente com taxa . É possível determinar um limiar epidêmico tal que para a epidemia pode se estabelecer no sistema, enquanto que para o estado absorvente é sempre alcançado. Enquanto em redes regulares o modelo SIS pertence à classe de universalidade de percolação direcionada, alguns expoentes críticos são diferentes e dependem das propriedades estruturais das redes complexas. Até mesmo a determinação do limiar epidêmico está longe de ser trivial nessas redes, e para isso são utilizadas teorias de campo médio, cujos resultados são comparados com simulações estocásticas. Fundamentalmente, as teorias HMF (do inglês heterogeneous mean-field) e QMF (do inglês quenched mean-field) levam a resultados conflitantes em redes em lei de potência com , e comportamentos assintóticos diferentes para . Ambas chegam ao mesmo resultado de que o limiar epidêmico tende a zero no limite termodinâmico para , já que diverge nesse intervalo, porém com escalas de tamanho finito diferentes para . Já para , enquanto a teoria HMF continua prevendo um limiar finito , a teoria QMF continua afirmando que o limiar tende a zero. Esse comportamento da teoria QMF está de acordo com os resultados analíticos exatos e simulações estocásticas. No Capítulo 4 introduzimos duas modificações nas regras do modelo SIS para investigar a robustez e fragilidade dos mecanismos de ativação em redes complexas. Enquanto no modelo SIS padrão (denominado por SIS-) um vértice infecta cada uma de suas conexões com taxa , no modelo modificado SIS- a infecção de um vértice suscetível ocorre com taxa quando pelo menos uma de suas conexões está infectada. Já no segundo modelo modificado SIS-, um vértice infectado infecta todas suas conexões suscetíveis com taxa ao mesmo tempo. Todos os três modelos levam aos mesmos limiares epidêmicos em suas respectivas teorias HMF e QMF. Porém, os modelos modificados acabam concordando com a teoria HMF para qualquer , diferente do que ocorre no modelo padrão, como mostrado na Figura 2. Essas diferenças são investigadas ao longo do capítulo e estão relacionadas com os diferentes mecanismos de ativação para cada e modelo SIS. Enquanto nos modelos modificados a dinâmica é dominada pelo o que ocorre em uma fração da rede (máximo -core, definido no Capítulo 2) para , isso só ocorre no modelo SIS- para . Para , os hubs são responsáveis pelo estado endêmico no modelo SIS-, possibilitando o espalhamento da epidemia para qualquer taxa no limite termodinâmico. Já para os modelos modificados SIS- e SIS- são ativados por uma fração coletiva da rede em um limiar finito. Esse trabalho ajuda a compreender os diferentes mecanismos de ativação de epidemias em redes complexas.
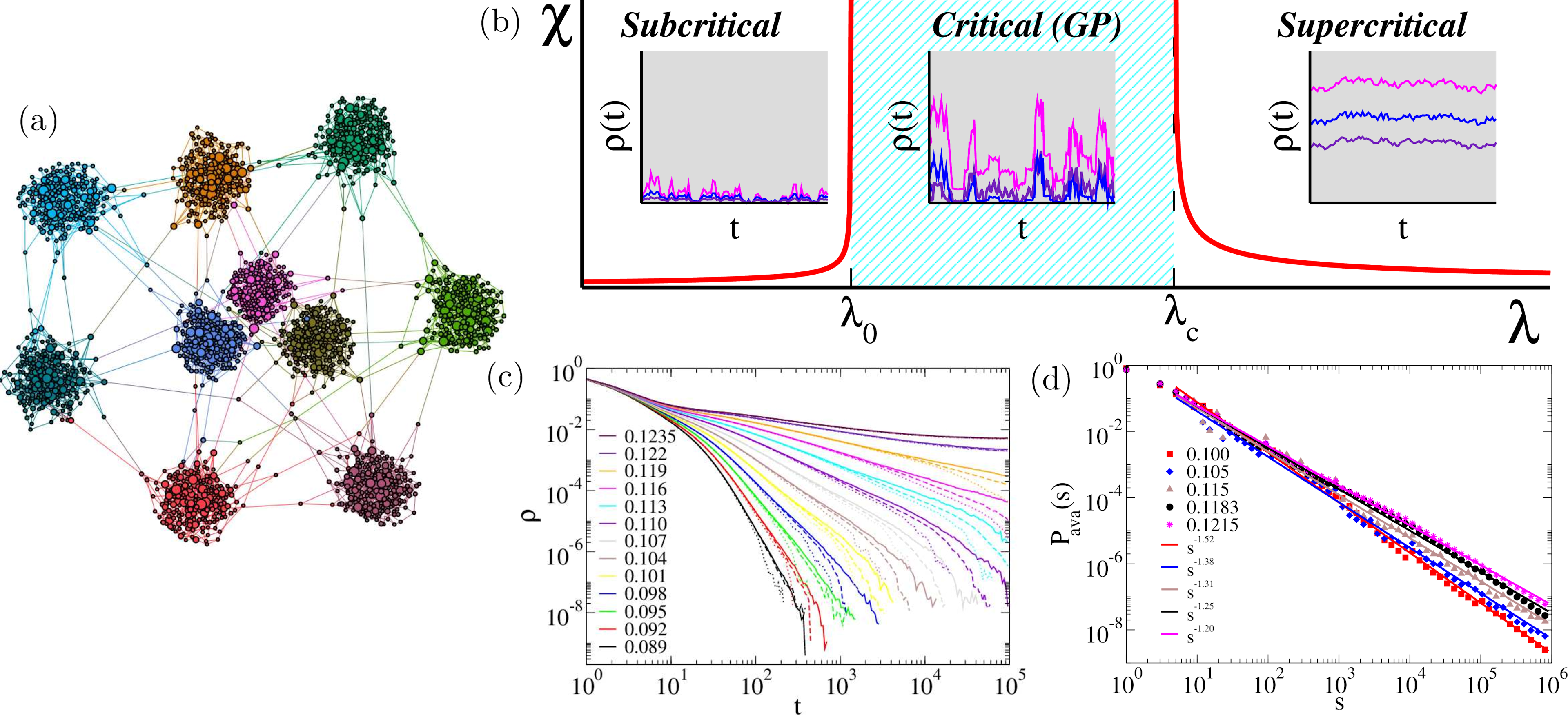
Figura 3: Fases de Griffiths em redes complexas modulares. (a) Representação de uma rede modular, (b) divergência da susceptibilidade na fase de Griffiths, (c) leis de potência no decaimento para diferentes taxas de infecção e (d) avalanches de atividades de tamanho para diferentes taxas . Mais detalhes nas Figuras 5.2, 5.11, 5.14 e 5.18 da Tese.
Outro estudo importante sobre a criticalidade de sistemas complexos é feito no Capítulo 5. Na Física da Matéria Condensada é conhecido que a desordem congelada pode levar às chamadas fases de Griffiths, nas quais ocorrem criticalidade dinâmica e alta sensibilidade a estímulos externos em uma região estendida do espaço de parâmetros, não apenas no ponto crítico. Redes complexas possuem essa desordem congelada, já que a heterogeneidade intrínseca a esses sistemas determina taxas de transições dependentes da conectividade de cada elemento. Em modelos epidêmicos com o SIS, vértices com grau maior podem infectar mais que os demais, por terem um maior número de conexões . Além disso, as taxas de cura podem ser diferentes para diferentes elementos, introduzindo outro tipo de desordem. Em particular, redes modulares são encontradas em sistemas reais como o cérebro e uma pergunta fundamental é como a criticalidade emerge nesses sistemas. Uma rede modular apresenta grupos de vértices altamente conectados entre si, com poucas ligações entre os módulos, como representado na Figura 3(a). Para processos epidêmicos, a criticalidade pode existir em um intervalo , definindo uma fase de Griffiths. Ao observar a fração de vértices infectados no estado estacionário em função da taxa são observadas leis de potência nesse intervalo do parâmetro de controle , não apenas para , no limiar epidêmico. A desordem congelada cria regiões raras, que sustentam atividade dinâmica por tempos longos. Além disso, medidas de função resposta como a suscetibilidade também divergem nessa fase de Griffiths, como representado na Figura 3(b). Foram estudadas diferentes configurações de redes complexas, mostrando que as fases de Griffiths podem ser observadas em redes modulares com as propriedades de mundo pequeno e livres de escala, como mostrado nas Figura 3(c,d). Decaimentos em lei de potência são encontrados para um grande intervalo de na Figura 3(c), e expoentes quase universais também são encontrados nas distribuições de avalanches de tamanho na Figura 3(d). Assim, a origem da criticalidade em sistemas modulares poderia ser explicada por meio dessas fases de Griffiths, reforçando também a hipótese do cérebro crítico existente na literatura.
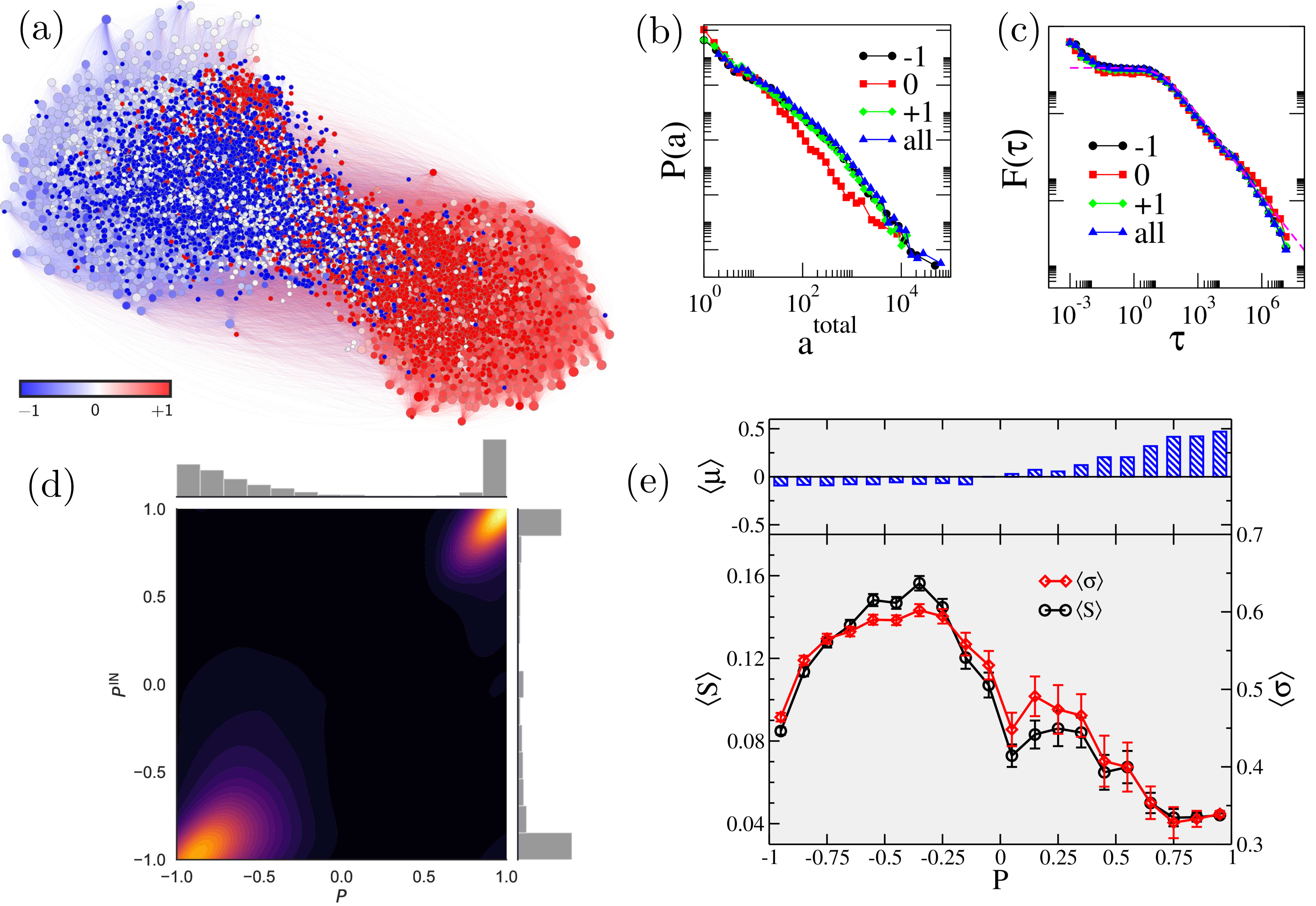
Figura 4: Propriedades estruturais e dinâmicas de câmaras de eco em uma rede de comunicação sobre política. (a) Representação da rede obtida, (b) distribuição do número de mensagens enviadas por cada usuário, (c) distribuição do intervalo de tempo entre mensagens, (d) mapa de calor do sentimento político das mensagens enviadas e recebidas , e (e) capacidade de espalhamento e média e variância do sentimento dos usuários atingidos em função do sentimento . Mais detalhes nas Figuras 6.8, 6.6, 6.10 e 6.14 da Tese.
Em seguida, no Capítulo 6 são estudadas redes de comunicação política obtidas a partir de dados do Twitter, uma rede social online. Essas redes sociais formam substratos gigantescos e altamente heterogêneos, com capacidade sem precedentes de propagar informação. Nelas é possível identificar a formação de câmaras de eco, nas quais indivíduos com opiniões parecidas interagem fortemente entre si, com poucas interações com os demais. Um exemplo é visto na Figura 4(a) para discussões a respeito do impeachment de Dilma Rousseff em 2016 no Brasil, com grupos contrários facilmente observados. Essa rede foi obtida depois de um longo processo de coleta e análise de mais de 48 milhões de mensagens entre março e dezembro de 2016, resultando em uma rede com distribuições em lei de potência claras do número de interações e intervalos entre mensagens para usuários com opiniões opostas e neutras, como mostrado nas Figura 4(b,c), respectivamente. Uma questão importante na literatura é como identificar essas câmaras de eco e quantificar a capacidade delas espalharem informações nesses sistemas. A cada usuário é atribuído um valor de sentimento definido pela média do sentimento de suas mensagens: -1 se a favor do impeachment, 0 se neutro ou relacionado ao assunto, e +1 se contra o impeachment. Também é possível determinar o sentimento como a média nas mensagens recebidas. Como resultado, vemos as câmaras de eco na Figura 4(d), já que usuários tendem a enviar e receber mensagens com o mesmo sentimento. Para estimar a capacidade de cada usuário para espalhar informações propomos um método inspirado em modelo epidêmicos como o SIS, seguindo explicitamente a sequência de interações obtidas a partir dos dados reais: no tempo , um usuário menciona outro e pode propagar a informação com taxa , e deixa de engajar em uma discussão com taxa . Para diferentes conjuntos de parâmetros e modelos dinâmicos encontramos os resultados da Figura 4(e), que mostra que a capacidade de espalhamento é correlacionada com a diversidade do sentimentos dos usuários atingidos a partir de uma mensagem iniciada em um usuário de sentimento da rede, medida pela variância do sentimento desses usuários atingidos. Além disso, a média do sentimento dos usuários atingidos é correlacionada com , evidenciando o efeito de câmera de eco. Esse efeito é mais forte nos usuários classificados como contra o impeachment, que possuem uma capacidade reduzida de espalhar mensagens, enquanto aqueles a favor do impeachment atingem uma diversidade maior de pessoas e, assim, conseguem espalhar muito mais na rede. O método proposto é robusto e permite quantificar esses efeitos nos mais diferentes contextos.
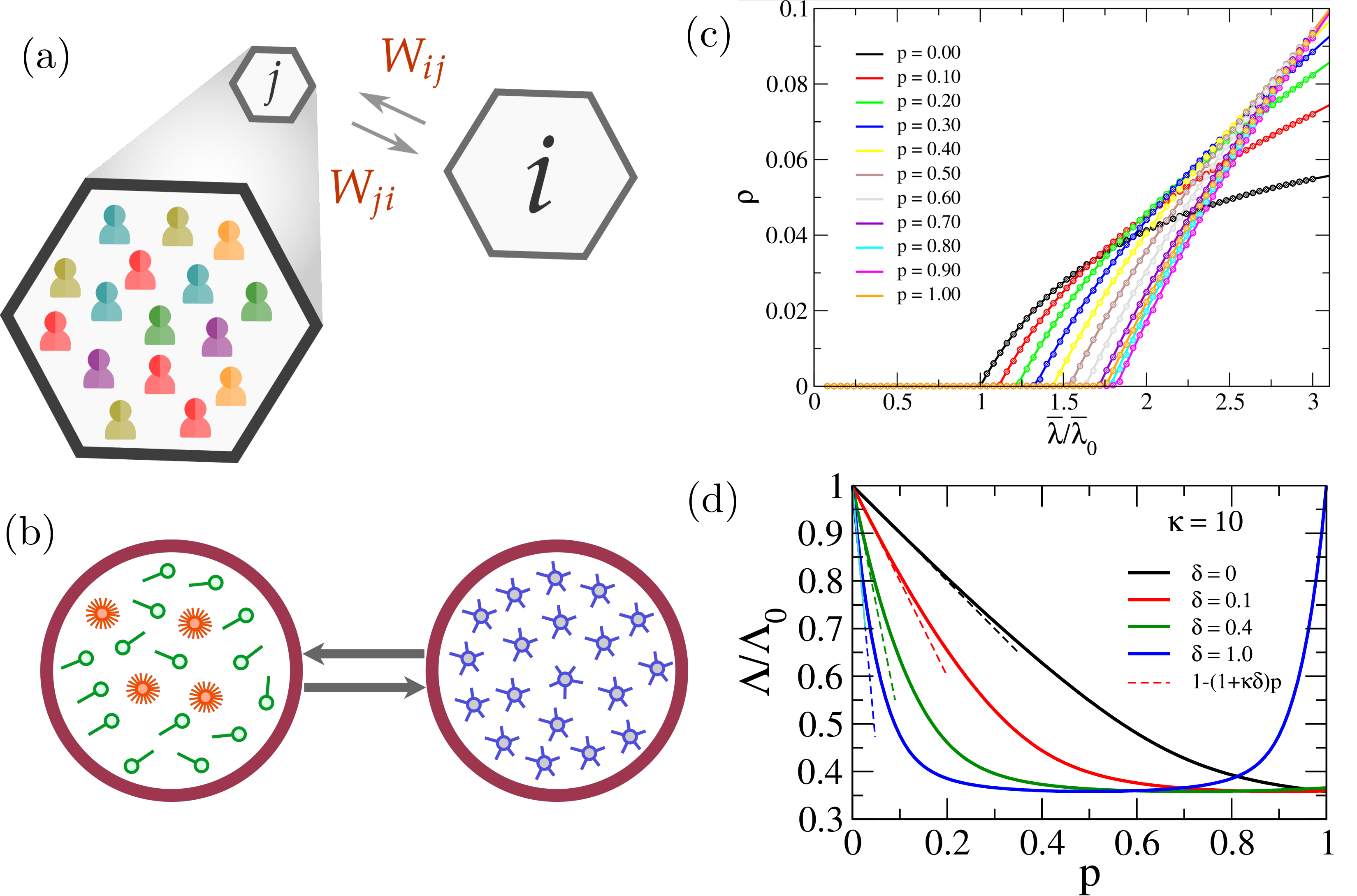
Figura 5: Efeitos da mobilidade na propagação de epidemias em metapopulações. (a) Representação do fluxo de uma população para , (b) subpopulações compostas de indivíduos com diferentes números de conexões, com indivíduos possuindo 1, 5 ou 20 conexões, (c) fração de indivíduos infectados em função da probabilidade de infecção , mostrando o crescimento do limiar epidêmico ao aumentar a mobilidade para simulações estocásticas (círculos) e integrações numéricas (linhas), e (d) comparação do maior autovalor (linhas sólidas) de uma matriz descrita na Tese com o resultado da teoria de perturbação (linhas tracejadas). Mais detalhes nas Figuras 7.1, 7.4, 7.7 e 7.10 da Tese.
Finalmente, no Capítulo 7 são apresentados modelos orientados por dados para lidar com situações mais realistas. O surgimento e acessibilidade de bancos de dados grandes sobre comportamentos sociais e mobilidade de indivíduos tem ajudado a entender a influência dos padrões de contato em modelos epidêmicos, estando disponíveis em diferentes escalas, e é um desafio introduzir essas informações em tratamentos analíticos desses modelos. Uma forma possível de representar matematicamente os padrões de mobilidade é por meio de metapopulações, que são redes complexas cujos vértices representam subpopulações, e arestas os fluxos de um local para outro , como na Figura 5(a). Dentro de cada vértice é necessário assumir um tipo de interação social, e uma primeira aproximação é considerar uma mistura homogênea. Muitos estudos na literatura mostraram que essas representações são muito efetivas para compreender surtos epidêmicos de doenças reais como H1N1 e COVID-19 [7,8,9]. Neste trabalho é utilizada uma abordagem baseada em cadeias de Markov microscópicas, escrevendo equações que incorporam explicitamente dados de demografia e mobilidade humana ao mesmo tempo que permitem obter resultados analíticos para, por exemplo, o limiar epidêmico em função da mobilidade. Diferente dos demais trabalhos da literatura, propomos uma adaptação ao introduzir contatos sociais heterogêneos dentro de cada população, como na Figura 5(b), descrevendo o número de contatos de cada indivíduo por distribuições como as em leis de potência. Os resultados obtidos a partir das equações diferenciais concordam com simulações estocásticas de Monte Carlo, e os limiares epidêmicos analíticos preveem corretamente o comportamento dinâmico em função da mobilidade parametrizada por um valor . Considerando contatos sociais homogêneos ou heterogêneos, é encontrado o fenômeno contra-intuitivo de detrimento epidêmico: o limiar epidêmico pode aumentar à medida que a mobilidade aumenta, dificultando o processo de espalhamento, como mostrado na Figura 5(c). A partir do modelo microscópico aqui descrito, é possível explicar esse comportamento pela competição de dois mecanismos: um de homogeneização, que acaba aumentando o limiar epidêmico -- semelhante ao que ocorre ao diminuir nos modelos em redes complexas --, e outro da nova distribuição espacial de indivíduos pelo sistema, favorecimento certos tipos de interações que fazem diminuir o limiar epidêmico, facilitando a propagação da epidemia. São efetuadas também análises perturbativas para comprovar analiticamente a existência desses mecanismos, como mostrado na Figura 5(d) para o maior autovalor de uma matriz, tal que . Esse modelo pode receber dados reais de demografia, mobilidade e padrões de contato para diferentes populações, assim como aqueles citados para o estudo da COVID-19 no Brasil [7] e Espanha [8,9].
Redes complexas descrevem diferentes sistemas naturais por meio de representações matemáticas apropriadas para lidar com inúmeros elementos interagindo entre si. O estudo de processos epidêmicos demanda ferramentas apropriadas para lidar com sistemas fora do equilíbrio, como no uso de equações mestras, cadeias de Markov e simulações estocásticas. Nesta Tese são estudados diferentes tipos de problemas, desde a criticalidade em modelos do tipo SIS [2], fases de Griffiths em redes complexas em lei de potência [3] e em redes complexas modulares [4], até aplicações para estudar câmaras de eco em redes sociais [5] e o efeito da mobilidade e padrões de contatos humanos em epidemias com metapopulações [6]. A importância e relevância desses trabalhos [1,2,3,4,5,6] é demonstrada por meio de outras contribuições [7,8,9,10,11]. também feitas durante o doutorado, além do impacto gerado quantificado pelo número de citações pelo Google Scholar.
Referências
[1] W. Cota and S. C. Ferreira, “Optimized Gillespie algorithms for the simulation of markovian epidemic processes on large and heterogeneous networks,” Comput. Phys. Commun. 219, 303–312 (2017).
[2] W. Cota, A. S. Mata, and S. C. Ferreira, “Robustness and fragility of the susceptible-infected-susceptible epidemic models on complex networks,” Phys. Rev. E 98, 012310 (2018).
[3] W. Cota, S. C. Ferreira, and G. Ódor, “Griffiths effects of the susceptible-infected-susceptible epidemic model on random power-law networks,” Phys. Rev. E 93, 032322 (2016).
[4] W. Cota, G. Ódor, and S. C. Ferreira, “Griffiths phases in infinite-dimensional, non-hierarchical modular networks,” Sci. Rep. 8, 9144 (2018).
[5] W. Cota, S. C. Ferreira, R. Pastor-Satorras, and M. Starnini, “Quantifying echo chamber effects in information spreading over political communication networks,” EPJ Data Sci. 8, 35 (2019).
[6] W. Cota, D. Soriano-Paños, A. Arenas, S. C. Ferreira, and J. Gómez-Gardeñes, “Infectious disease dynamics in metapopulations with heterogeneous transmission and recurrent mobility,” New Journal of Physics 23, 073019 (2021).
[7] G. S. Costa, W. Cota, and S. C. Ferreira, “Outbreak diversity in epidemic waves propagating through distinct geographical scales,” Phys. Rev. Research 2, 043306 (2020).
[8] A. Arenas, W. Cota, J. Gomez-Gardenes, S. Gómez, C. Granell, J. T. Matamalas, D. Soriano-Panos, and B. Steinegger, “A mathematical model for the spatiotemporal epidemic spreading of COVID19,” medRxiv, 2020.03.21.20040022 (2020).
[9] A. Arenas, W. Cota, J. Gómez-Gardeñes, S. Gómez, C. Granell, J. T. Matamalas, D. Soriano-Paños, and B. Steinegger, “Modeling the spatiotemporal epidemic spreading of COVID-19 and the impact of mobility and social distancing interventions,” Phys. Rev. X 10, 041055 (2020).
[10] D. H. Silva, S. C. Ferreira, W. Cota, R. Pastor-Satorras, and C. Castellano, “Spectral properties and the accuracy of mean-field approaches for epidemics on correlated power-law networks,” Phys. Rev. Research 1, 033024 (2019).
[11] W. Cota, “Monitoring the number of COVID-19 cases and deaths in brazil at municipal and federative units level,” (2020), 10.1590/scielopreprints.362.